Pelajaran Matematika Soal UAS Kelas 10

 

Berikut adalah contoh soal latihanUAS matematika wajib untuk kelas 10 semseter ganjil (1)

﷽

Pelajari

Pelajaran IPA Fisika Fluida Dinamis

Fluida adalah zat yang mudah mengalir, dalam hal ini yang termasuk fluida adalah zat cair dan gas. Fluida dinamis adalah fluida yang sedang bergerak atau sedang mengalir.

Pelajari

Pelajaran Matematika Matriks

Matriks adalah sekumpulan bilangan maupun simbol yang disusun dalam baris dan kolom serta dibatasi dengan tanda kurung. Matriks dapat membentuk persegi ataupun persegi panjang.

Pelajari

Pelajaran Matematika Trigonometri Analitika

 

Trigonometri adalah cabang ilmu matematika yang mempelajari hubungan panjang dan sudut segitiga. Materi lanjutan setelah trigonometri dasar adalah trigonometri analitika yang meliputi rumus jumlah, selisih maupun perkalian sudut dan perbandingan trigonometrinya.

Pelajari

Pelajaran IPA Fisika Dinamika Rotasi

 

Gerak rotasi benda adalah gerak suatu benda mengitari suatu poros. Dinamika rotasi mempelajari gerak rotasi benda dengan penyebabnya yaitu  torsi atau

Pelajari

Pelajaran Matematika Fungsi Trigonometri

 

Fungsi trigonometri adalah enam fungsi dasar yang memiliki nilai input domain sebagai sudut segitiga siku-siku, dan jawaban numerik sebagai rentang.

Pelajari

Pelajaran Matematika Notasi Sigma

 Notasi Sigma adalah metode penjumlahan bilangan-bilangan berurut yang mengikuti pola tertentu dan dilambangkan dalam simbol Σ.

Pelajari

Pelajaran Matematika Logika Matematika

Logika Matematika adalah metode berpikir untuk memisahkan penalaran yang benar dan penalaran yang salah pada suatu pernyataan matematis. 

Selanjutnya dalam logika matematika dipelajari 4 macam kalimat majemuk yang dalam penyelesaiannya diperlukan tabel kebenaran seperti berikut:  

Pelajari

Pelajaran Matematika VEKTOR

 

vektor, dalam matematika, adalah besaran yang memiliki besar dan arah tetapi tidak memiliki posisi. digambarkan dengan ruas garis yang ujungnya berupa panah untuk menunjukkan arah.

Pelajari

Rumus Kimia Dan Nomenklatur Senyawa Sederhana

Senyawa adalah gabungan dua atau lebih unsur kimia dengan perbandingan tertentu. Jenis dan perbandingan jumlah unsur penyusun suatu senyawa diekspresikan dalam suatu rumus kimia dengan aturan-aturan tertentu.

Pelajari

Pelajaran Kimia Larutan Elektrolit dan Reaksi Redoks

Larutan elektrolit adalah larutan yang dapat menghantarkan listrik karena adanya ion-ion yang dapat bergerak dengan bebas. Reaksi redoks adalah reaksi yang melibatkan pengikatan dan pelepasan elektron.

Pelajari

Pelajaran IPA Fisika tentang Gravitasi

Gravitasi (dari bahasa Latin gravitas 'berat'), adalah fenomena alam di mana semua benda dengan massa atau energi—termasuk planet, bintang, galaksi, dan bahkan cahaya—tarik menarik satu sama lain. 

Pelajari

Pelajaran Matematika Perbandingan Trigonometri

Perbandingan trigonometri adalah perbandingan antara sisi-sisi segitiga siku-siku. Perbandingan ini diberikan oleh fungsi trigonometri berikut dari sudut yang diketahui A, di mana a, b dan c mengacu pada panjang sisi

Pelajari

Pelajaran IPA Fisika Arus bolak-balik (AC)

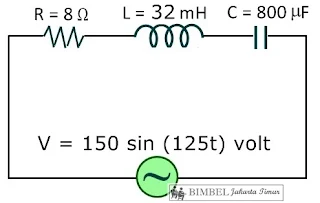
Berikut adalah Soal Arus dan Tegangan Bolak-balik untuk kelas 12 berikut jawaban dan pembahasan

Soal Arus dan Tegangan Bolak-balik Kelas 12

Apa arus bolak-balik?

Arus bolak-balik dapat didefinisikan sebagai arus yang mengubah besarnya dan polaritas pada interval waktu reguler. Ini juga dapat didefinisikan sebagai arus listrik yang berulang kali mengubah atau membalikkan arahnya berlawanan dengan arus searah atau Arus searah (DC) yang selalu mengalir dalam satu arah.

Pelajari

Pelajaran IPA Klasifikasi Materi dan Perubahannya

Tiga klasifikasi materi dalam bentuk fisik berbeda di sebagian besar lingkungan adalah : padat, cair, dan gas. Di lingkungan ekstrim, klasifikasi materi lain mungkin ada yang seperti plasma, kondensat Bose-Einstein, dan bintang neutron.

Pelajari

Pelajaran IPA Fisika Gerak Parabola

Gerak parabola yaitu gerak yang lintasannya bentuk parabola. Gerak parabola ini perpaduan gerak lurus beraturan (GLB) pada sumbu horisontal dan gerak lurus berubah beraturan (GLBB) pada sumbu vertikal. Percepatan yang berpengaruh pada sumbu vertikal adalah percepatan gravitasi.

Pelajari

Pelajaran Matematika Grafik Fungsi Kuadrat

Fungsi kuadrat yaitu fungsi yang persamaannya memiliki variabel dengan pangkat tertingginya 2. Dalam materi fungsi kuadrat kita pelajari ciri-ciri grafik fungsi kuadrat,sumbu simetri, nilai optimum (maksimum atau minimum) serta titik potongnyaterhadap sumbu pada koordinat kartesius. 

Persamaan umumfungsi kuadrat adalah :

F(x)=ax² + bx + c atau y=ax² + bx + c

Variabel x padafungsi kuadrat adalah variabel bebas sedangkan y sebagai variabel terikat. adan b sebagai koefisien dimana a ≠ 0  danc sebagai konstanta.

Grafik fungsi kuadrat adalah grafik berbentuk kurva parabola yangdihasilkan dari persamaan kuadrat yang digambarkan pada bidang kartesius.

Fungsi kuadrat

Fungsi kuadrat digunakan di berbagai bidang teknik dan sains untuk mendapatkan nilai parameter yang berbeda. Secara grafis, mereka diwakili oleh parabola. Bergantung pada koefisien derajat tertinggi, arah kurva ditentukan. Kata “Quadratic” berasal dari kata “Quad” yang berarti persegi. Dengan kata lain, fungsi kuadrat adalah "fungsi polinomial derajat 2." Ada banyak skenario di mana fungsi kuadrat digunakan. Tahukah Anda bahwa ketika sebuah roket diluncurkan, jalurnya dijelaskan oleh solusi fungsi kuadrat?

Fungsi kuadrat adalah fungsi polinomial dengan satu atau lebih variabel yang eksponen tertinggi variabelnya adalah dua. Karena suku derajat tertinggi dalam fungsi kuadrat adalah derajat kedua, maka disebut juga polinomial derajat 2. Sebuah fungsi kuadrat memiliki minimal satu suku derajat kedua.

Pada artikel ini, kita akan menjelajahi dunia fungsi kuadrat dalam matematika. Anda akan belajar tentang grafik fungsi kuadrat, rumus fungsi kuadrat, dan fakta menarik lainnya seputar topik ini.

Grafik fungsi kuadrat adalah parabola, dan bagian-bagiannya memberikan informasi yang berharga tentang fungsi tersebut.

Fitur Parabola

Parabola memiliki beberapa fitur yang dapat dikenali yang mencirikan bentuk dan penempatannya pada bidang Cartesian.

Puncak (vertex)

Salah satu fitur penting dari parabola adalah memiliki titik ekstrem, yang disebut titik. Jika parabola terbuka, simpul mewakili titik terendah pada grafik, atau nilai minimum fungsi kuadrat. Jika parabola terbuka ke bawah, simpul mewakili titik tertinggi pada grafik, atau nilai maksimum. Dalam kedua kasus, simpul adalah titik balik pada grafik.

Sumbu Simetri

Parabola juga memiliki sumbu simetri yang sejajar dengan sumbu y. Sumbu simetri adalah garis vertikal yang ditarik melalui titik sudut.

Perpotongan y

Perpotongan y adalah titik di mana parabola memotong sumbu y. Tidak boleh ada lebih dari satu titik seperti itu, untuk grafik fungsi kuadrat. Jika ada, kurva tidak akan menjadi fungsi, karena akan ada dua nilai y untuk satu nilai x, pada nol.

Perpotongan x

Perpotongan x adalah titik potong parabola terhadap sumbu x. Jika ada, perpotongan x mewakili nol, atau akar, dari fungsi kuadrat, nilai x di mana y=0. Mungkin ada nol, satu, atau dua perpotongan x. Jumlah perpotongan x bervariasi tergantung pada lokasi grafik.

Persamaan polinomial dengan pangkat tertinggi dari variabelnya adalah 2 disebut fungsi kuadrat. Kami tiba di grafik berikut ketika kami menggambar fungsi kuadrat seperti y = x^2:

Kita dapat dengan mudah melihat bahwa kita tidak berhadapan dengan garis lurus tetapi parabola, sehingga disebut sebagai fungsi non-linier. Ketika seseorang memiliki koefisien positif sebelum x2 kita memiliki nilai minimum, dan jika kita memiliki koefisien negatif, kita memiliki nilai maksimum sebagai gantinya. Lihat grafik di bawah ini di mana y = -x^2:

Aturan praktis mengingatkan kita bahwa ketika kita memiliki simbol positif sebelum x^2 kita mendapatkan ekspresi bahagia pada grafik :) dan simbol negatif membuat ekspresi sedih :( 

Keterangan Pelajaran Selanjutnya dalam bentuk grafik dan rumus :

Grafik Fungsi Kuadrat

Tag:

contoh soal grafik fungsi kuadrat

contoh soal fungsi kuadrat dan grafik parabola

grafik fungsi kuadrat f

contoh soal grafik fungsi kuadrat

grafik fungsi kuadrat kelas 9

contoh soal grafik fungsi kuadrat kelas 9

sifat grafik fungsi kuadrat

kesimpulan grafik fungsi kuadrat

Pelajari

Pelajaran IPA Gerak Melingkar Beraturan

Gerak Melingkar: gerak yang lintasannya melingkar atau mengelilingi titik yang tetap gerak melingkar terdiri dari gerak melingkar beraturan yang mempunyai kecepatan sudut tetap dan gerak melingkar berubah beraturan yang percepatan sudutnya tetap.

Apa itu Gerak Melingkar Beraturan?

• Gerak benda yang mengikuti lintasan melingkar disebut gerak melingkar. Sekarang, gerak suatu benda yang bergerak dengan kecepatan konstan sepanjang lintasan melingkar disebut Gerak Melingkar Beraturan. Di sini, kecepatannya konstan tetapi kecepatannya berubah.
• Gerak Melingkar Beraturan adalah gerak 2 dimensi di mana benda bergerak dengan kecepatan seragam dalam arah melingkar yang tetap tetapi karena arah benda terus berubah di setiap titik, kecepatannya juga terus berubah, arahnya di setiap titik adalah arah menuju garis singgung.
• Gerak melingkar adalah bagian dari kehidupan. Planet-planet mengorbit matahari dalam gerakan melingkar. Sebuah mobil melengking saat melewati tikungan juga dalam gerakan melingkar. Dan jika kita pernah bermain tenis rumput, jenis dengan bola di atas tali yang terbang di sekitar tiang, maka kita akan mengalami contoh lain dari gerakan melingkar. Jika kita bergerak dengan kecepatan konstan dalam lingkaran kita, maka gerakan tersebut dikatakan beraturan.
• Gerak melingkar beraturan adalah gerak melingkar dengan kecepatan tetap. Hal ini terjadi karena adanya gaya sentripetal, yaitu gaya yang mengarah ke pusat lingkaran. Secara matematis, sebuah benda yang bergerak melingkar beraturan memiliki gaya total menuju pusat lingkaran, vektor percepatan menuju pusat lingkaran, dan kecepatan singgung lingkaran.

Pada gerak melingkar beraturan, benda bergerak pada lintasan melingkar dengan kecepatan tetap. Ini berarti bahwa benda akan menempuh jarak yang sama pada keliling lingkaran dalam selang waktu yang sama. Pada gerak melingkar tak beraturan, kecepatan benda berubah.

Meskipun kelajuan konstan dalam gerak melingkar beraturan, ada perubahan terus menerus dalam arah gerak, seperti yang telah kita bahas di bagian sebelumnya. Oleh karena itu, kecepatan suatu benda yang mengalami gerak melingkar beraturan juga berubah terus menerus. Karena perubahan arah kecepatan, benda mengalami percepatan yang disebut percepatan sentripetal.

Dari hukum gerak pertama Newton, kita tahu bahwa benda tidak dapat mengubah arah geraknya sendiri. Sebuah kekuatan eksternal diperlukan untuk tujuan ini. Gaya luar yang membuat benda tetap bergerak sepanjang lintasan melingkar disebut gaya sentripetal.

Benda yang mengalami gerak melingkar beraturan dapat digambarkan sebagai gerak suatu benda dalam lingkaran dengan kelajuan tetap. Saat sebuah objek bergerak dalam lingkaran, ia terus-menerus mengubah arahnya. Pada semua contoh, objek bergerak bersinggungan dengan lingkaran. Karena arah vektor kecepatan sama dengan arah gerak benda, vektor kecepatan juga diarahkan bersinggungan dengan lingkaran. Animasi di sebelah kanan menggambarkan ini melalui panah vektor.

Sebuah benda yang bergerak melingkar mengalami percepatan. Benda yang dipercepat adalah benda yang mengubah kecepatannya - baik kecepatan (yaitu, besarnya vektor kecepatan) atau arah. Sebuah benda yang mengalami gerak melingkar beraturan bergerak dengan kecepatan tetap. Namun, itu semakin cepat karena perubahan arahnya. Arah percepatannya ke dalam. Animasi di sebelah kanan menggambarkan ini melalui panah vektor.

Karakteristik gerak akhir untuk suatu benda yang mengalami gerak melingkar beraturan adalah gaya total. Gaya total yang bekerja pada benda semacam itu diarahkan ke pusat lingkaran. Gaya total dikatakan sebagai gaya ke dalam atau gaya sentripetal. Tanpa gaya dalam seperti itu, sebuah benda akan terus dalam garis lurus, tidak pernah menyimpang dari arahnya. Namun, dengan gaya total ke dalam yang diarahkan tegak lurus terhadap vektor kecepatan, objek selalu mengubah arahnya dan mengalami percepatan ke dalam.

Dalam fisika, gerak melingkar beraturan menggambarkan gerak benda yang melintasi lintasan melingkar dengan kecepatan konstan. Karena benda menggambarkan gerak melingkar, jaraknya dari sumbu rotasi tetap konstan sepanjang waktu. Meskipun kecepatan benda adalah konstan, kecepatannya tidak konstan: kecepatan, besaran vektor, bergantung pada kecepatan benda dan arah perjalanannya. Perubahan kecepatan ini menunjukkan adanya percepatan; percepatan sentripetal ini besarnya konstan dan diarahkan setiap saat menuju sumbu rotasi. Percepatan ini, pada gilirannya, dihasilkan oleh gaya sentripetal yang besarnya juga konstan dan diarahkan ke sumbu rotasi.

Dalam kasus rotasi di sekitar sumbu tetap dari benda tegar yang tidak terlalu kecil dibandingkan dengan jari-jari lintasan, setiap partikel benda menggambarkan gerak melingkar beraturan dengan kecepatan sudut yang sama, tetapi dengan kecepatan dan percepatan yang bervariasi dengan posisi terhadap sumbu.

Kasus paling sederhana dari gerak melingkar adalah gerak melingkar beraturan, di mana suatu benda menempuh lintasan melingkar dengan kecepatan konstan. Perhatikan bahwa, tidak seperti kecepatan, kecepatan linier suatu benda yang bergerak melingkar selalu berubah karena selalu berubah arah. Kita tahu dari kinematika bahwa percepatan adalah perubahan kecepatan, baik dalam besaran atau arah atau keduanya. Oleh karena itu, suatu benda yang mengalami gerak melingkar beraturan selalu mengalami percepatan, meskipun besar kecepatannya tetap.

Kita sebenarnya mengalami akselerasi ini sendiri setiap kali kita mengendarai mobil saat berbelok di tikungan. Jika kita memegang kemudi dengan stabil selama belokan dan bergerak dengan kecepatan konstan, kita melakukan gerakan melingkar yang seragam. Apa yang kita perhatikan adalah perasaan meluncur (atau terlempar, tergantung pada kecepatan) menjauh dari pusat belokan. Ini bukan gaya aktual yang bekerja pada kita —itu hanya terjadi karena tubuh kitaingin terus bergerak dalam garis lurus (sesuai hukum pertama Newton) sedangkan mobil membelokkan jalur garis lurus ini. Di dalam mobil tampak seolah-olah kita dipaksa menjauh dari pusat belokan. Gaya ini dikenal sebagai gaya sentrifugal. Semakin tajam kurva dan semakin besar kecepatan kita, semakin terlihat efek ini.

Jika sebuah partikel bergerak dalam lingkaran, ia harus memiliki beberapa percepatan yang bekerja menuju pusat yang membuatnya bergerak di sekitar pusat. Karena percepatan ini tegak lurus terhadap kecepatan partikel setiap saat, itu hanya mengubah arah kecepatan dan bukan besaran dan itulah sebabnya gerakannya adalah gerakan melingkar beraturan. Kami menyebutnya percepatan sentripetal (atau percepatan radial), dan gaya yang bekerja menuju pusat disebut gaya sentripetal.

Dalam kasus gerak melingkar beraturan, percepatannya adalah:

• ar = v2r = ω2r
• Jika massa partikel adalah m, kita dapat mengatakan dari hukum gerak kedua bahwa:
• F = ma
• mv2r= mω2r

Ini bukan gaya yang secara khusus terjadi begitu saja, sebenarnya gaya seperti tegangan atau gesekan dapat menjadi penyebab timbulnya gaya sentripetal. Ketika kendaraan berbelok di jalan, itu adalah gaya gesekan antara ban dan tanah yang memberikan gaya sentripetal yang diperlukan untuk berbelok.

CATATAN

Jadi jika sebuah partikel bergerak dalam gerakan melingkar beraturan:

1) Kecepatannya tetap

2) Kecepatan berubah setiap saat

3) Tidak ada percepatan tangensial

4) Percepatan radial (sentripetal) = 2r

5)v=ωr

Dalam kasus gerakan melingkar yang tidak seragam, ada beberapa percepatan tangensial yang menyebabkan kecepatan partikel meningkat atau menurun. Percepatan yang dihasilkan adalah jumlah vektor percepatan radial dan percepatan tangensial.

Contoh Gerak Melingkar Berseragam

Berikut adalah contoh gerak melingkar beraturan:

• Gerak satelit buatan mengelilingi bumi merupakan contoh gerak melingkar beraturan. Gaya gravitasi dari bumi membuat satelit tetap berada pada orbit melingkar mengelilingi bumi.
• Pergerakan elektron di sekitar nukleusnya.
• Gerakan bilah kincir angin.
• Ujung jarum detik jam tangan dengan dial melingkar menunjukkan gerakan melingkar yang seragam.

Ada banyak contoh fisik gaya sentripetal, dan kita tidak dapat sepenuhnya mengeksplorasi masing-masing. Dalam kasus sebuah mobil bergerak di sekitar tikungan, gaya sentripetal disediakan oleh gaya gesekan statis ban mobil di jalan. Meskipun mobil bergerak, gaya sebenarnya tegak lurus terhadap gerakannya, dan merupakan gaya gesekan statis. Dalam kasus pesawat terbang berputar di udara, gaya sentripetal diberikan oleh gaya angkat yang diberikan oleh sayap miringnya. Akhirnya, dalam kasus sebuah planet berputar mengelilingi matahari, gaya sentripetal diberikan oleh gaya tarik gravitasi antara kedua benda.

Dengan pengetahuan tentang kekuatan fisik seperti ketegangan, gravitasi dan gesekan, gaya sentripetal menjadi perpanjangan dari Hukum Newton. Ini istimewa, bagaimanapun, karena secara unik ditentukan oleh kecepatan dan jari-jari gerakan melingkar beraturan. Semua Hukum Newton masih berlaku, diagram benda bebas masih merupakan metode yang valid untuk menyelesaikan masalah, dan gaya masih dapat diselesaikan menjadi komponen-komponen. Jadi hal yang paling penting untuk diingat mengenai gerak melingkar beraturan adalah bahwa itu hanyalah bagian dari topik dinamika yang lebih besar.

Pertanyaan: Apakah ada percepatan dalam gerak melingkar beraturan?

Jawab: Ya!! Kecepatan berubah karena arah berubah. Namun kecepatannya tetap konstan.

Soal: Sebuah bola diputar melingkar. Jika tali dilepaskan saat bola berada pada posisi yang ditunjukkan, jalur manakah yang akan dilalui bola?

Jawaban: Jika tali dilepaskan tidak ada gaya untuk membelokkan lintasan bola, sehingga bola akan terus bergerak lurus mengikuti lintasan 2.

Besaran Dasar dalam Gerak Melingkar

• r = jari-jari lintasan melingkar
• T = periode, waktu untuk berputar sekali
• v = kecepatan linier
• a = percepatan linier

3 besaran pertama dihubungkan oleh: v T = 2πr.

Percepatan Sentripetal

• Fitur penting dari gerak melingkar beraturan adalah percepatan sentripetal ac yang mengarah secara radial ke dalam dan menjaga partikel pada jalur melingkar.
• Percepatan sentripetal adalah ac=v2/r (radial ke dalam)

Variabel Sudut dan Linear

Gerak melingkar lebih berguna dijelaskan dengan menggunakan variabel sudut. Alih-alih jarak yang ditempuh, kami fokus pada sudut rotasi. Variabel sudut ini adalah:

• Jarak: s = rθ  θ = posisi sudut
• Kecepatan: v = rω = kecepatan sudut
• Percepatan: di = rα; α= percepatan sudut (tangensial)

Percepatan tangensial melibatkan percepatan atau perlambatan suatu benda saat bergerak sepanjang jalur melingkar,

Penting: Dalam gerak melingkar beraturan di = 0, sedangkan ac tidak nol dan menunjuk ke arah radial.

Sebuah benda yang bergerak pada lintasan melingkar mengalami gerak melingkar. Jika kecepatan benda konstan, itu adalah gerak melingkar beraturan.

Sebuah benda yang bergerak melingkar beraturan memang mengalami percepatan, meskipun kecepatannya tetap. Ingat, percepatan adalah perubahan kecepatan, dan kecepatan terdiri dari kecepatan dan arah. Agar objek bergerak dalam lingkaran, arah kecepatannya harus berubah secara konstan. Perubahan arah ini adalah percepatan, yang disebut percepatan sentripetal ("sentripetal" berarti "menuju pusat"). Untuk sebuah benda yang bergerak pada lintasan melingkar, vektor percepatan sentripetal selalu mengarah ke pusat lingkaran.

Seperti jenis percepatan lainnya, percepatan sentripetal disebabkan oleh gaya (disebut gaya sentripetal). Vektor gaya sentripetal juga selalu mengarah ke pusat lingkaran.

Agar suatu benda dapat bergerak dalam lintasan melingkar, gaya total yang bekerja pada benda harus berupa gaya sentripetal (gaya yang selalu mengarah ke pusat). Ketika beberapa gaya bekerja pada sebuah benda yang bergerak melingkar, gaya-gaya tersebut harus bertambah menjadi gaya sentripetal. Penting untuk dipahami bahwa gaya sentripetal bukanlah gaya terpisah yang bekerja pada suatu benda. Ini adalah gaya total yang mengikuti aturan tertentu: selalu mengarah ke pusat jalur melingkar.

Pengertian gerak melingkar

Ketika sebuah benda bergerak dalam lintasan melingkar, kita menyebutnya gerak melingkar. Beberapa contoh umum gerak melingkar adalah:

• Sebuah mobil balap bergerak pada kurva melingkar;
• Satelit buatan yang berputar mengelilingi bumi;
• Ujung jarum menit/detik dari sebuah jam; dan
• Memutar batu yang diikat dengan tali.
• Gerak melingkar suatu benda dapat berupa gerak melingkar beraturan atau gerak melingkar tak beraturan.

Dalam gerak melingkar, arah gerak berubah terus menerus. Setiap saat, arah gerak benda yang bergerak dalam lintasan melingkar adalah sepanjang garis singgung lingkaran pada saat itu.

Cara yang lebih mudah untuk memvisualisasikan konsep ini adalah dengan membayangkan sebuah batu yang dililitkan pada seutas tali; ketika tali putus, batu terbang ke arah tangensial.

Hukum I Newton tentang gerak menyatakan bahwa suatu benda yang bergerak dengan kecepatan konstan akan melanjutkan gerak itu kecuali jika ada gaya luar yang bekerja. Ini berarti bahwa gerak melingkar hanya dapat terjadi jika ada gaya "pencari pusat" – jika tidak, benda-benda hanya akan bergerak dalam garis lurus, bukan garis lengkung dari sebuah lingkaran. Sentripetal berarti 'pencarian pusat', jadi gaya sentripetal digunakan untuk merujuk pada gaya yang dialami oleh benda yang bergerak dalam lingkaran. Misalnya, ketika seseorang memutar bola yang diikatkan pada tali secara horizontal di atas kepalanya, tali tersebut mentransmisikan gaya sentripetal dari otot-otot tangan dan lengan, menyebabkan bola bergerak dalam lintasan melingkar.

Gaya sentripetal menyebabkan percepatan sentripetal. Dalam kasus khusus gerakan melingkar Bumi mengelilingi Matahari – atau gerakan melingkar satelit apa pun di sekitar benda langit mana pun – gaya sentripetal yang menyebabkan gerakan tersebut adalah hasil dari gaya tarik gravitasi di antara keduanya.

Gerak pada bidang adalah ketika suatu benda bergerak dalam dua koordinat, misalkan x, y atau y, z, dan seterusnya. Salah satu contoh Gerak 2 Dimensi adalah Gerak Proyektil dimana benda bergerak baik dalam arah horizontal maupun vertikal. Gerak melingkar beraturan adalah contoh lain dari gerak 2 dimensi, di mana benda bergerak dengan kecepatan seragam dalam gerak melingkar sedangkan kecepatannya terus berubah di setiap titik karena arah vektor kecepatan terus berubah.

Ketika benda bergerak melingkar, pada setiap titik, beberapa percepatan dialami oleh benda, percepatan bekerja menuju pusat lingkaran yang membuat benda bergerak dalam lingkaran itu. Percepatan tersebut dikenal sebagai Percepatan radial atau Percepatan sentripetal.

Dalam gerak melingkar beraturan, gaya yang bekerja menuju pusat disebut gaya sentripetal dan untuk mengimbangi gaya tersebut, gaya yang bekerja di luar lingkaran dikenal sebagai gaya sentrifugal.

Catatan:

• Gaya sentripetal selalu bekerja menuju pusat.
• Arah Kecepatan selalu bersinggungan dengan lingkaran di semua titik.
• Vektor percepatan akan selalu tegak lurus terhadap vektor kecepatan dan karenanya, akan selalu mengarah ke pusat.
• Kecepatan sudut diberikan sebagai, w = v/r
• dimana, w = kecepatan sudut
• v = besar kecepatan
• r = jari-jari lingkaran
• Besarnya percepatan diberikan sebagai, a=v2/r
• Nilai percepatan sudut selalu nol pada gerak melingkar beraturan karena kecepatan sudutnya konstan.

Hal yang menarik tentang gerak melingkar adalah menunjukkan dengan sangat jelas mengapa penting untuk mengetahui perbedaan antara skalar dan vektor. Kecepatan adalah skalar, sedangkan kecepatan adalah vektor - kecepatan harus mencakup arah, bukan hanya angka. Kecepatan suatu benda dalam gerak melingkar beraturan adalah konstan karena bagaimanapun juga itulah yang membuatnya seragam. Tapi kecepatannya selalu berubah. Satelit atau mobil atau burung yang bergerak dalam gerakan melingkar selalu berubah arah, sehingga kecepatannya terus berubah. Ini menunjukkan mengapa suatu benda dapat memiliki percepatan bahkan pada kecepatan konstan.

Gaya Sentripetal vs. Gaya Sentrifugal

Sebuah benda yang bergerak melingkar tetap berada dalam lingkaran tersebut karena adanya gaya sentripetal. Gaya sentripetal adalah gaya yang arahnya menuju pusat lingkaran. Tapi ini tampaknya bertentangan dengan pengalaman banyak orang.

Katakanlah kita berada di kursi penumpang mobil, ketika berbelok tajam ke kiri. Di mana kita didorong? Jika kita memiliki ingatan yang baik untuk hal semacam ini, kita mungkin akan menjawab bahwa kita didorong ke kanan - atau dengan kata lain, kitadidorong ke luar lingkaran. Jadi pasti, gaya itu menjauhi pusat lingkaran, bukan ke arahnya. Ini adalah definisi gaya sentrifugal, gaya yang menjauhi pusat lingkaran.

Tapi gaya sentrifugal tidak benar-benar ada. Saat kita duduk di dalam mobil yang bergerak dalam garis lurus, tubuh  kita akan terus berjalan dalam garis lurus. Hukum 1 Newton, yang kita bicarakan dalam pelajaran lain, mengatakan bahwa benda yang bergerak tetap bergerak, benda yang diam tetap diam, kecuali jika ditindaklanjuti oleh gaya yang tidak seimbang. Jadi, ketika mobil berbelok, tubuh kita akan tetap lurus. Tubuh kita berjalan lurus, tetapi mobil berbelok, menyebabkan kita menabrak bagian luar tikungan. Tetapi mobil sebenarnya menahan kita di dalam lingkaran, jadi meskipun kita merasakan tekanan dari pintu mobil, gaya yang dialami tubuh kita mengarah ke pusat lingkaran - itu sentripetal. Jika tidak, kita hanya akan terus berjalan dengan baik, rapi, dan lurus.

persamaan

Ada dua persamaan utama yang perlu kita ketahui tentang gerak melingkar. Yang pertama membantu kita menghitung ukuran gaya sentripetal itu. Dikatakan bahwa gaya sentripetal, Fc, diukur dalam newton, sama dengan massa benda yang bergerak dalam lingkaran, m, dikalikan dengan kecepatan benda saat mengelilingi lingkaran, v, diukur dalam meter per detik, kuadrat (hanya kecepatan yang dikuadratkan), dibagi dengan jari-jari lingkaran, diukur dalam meter.

Agar dapat lebih memahami, tidak ada salahnya kita memperlajari lebih jauh lagi, melalui soal dan pembahasan:

Soal Gerak Melingkar Beraturan

Tag:

sebuah benda yang mengalami gerak melingkar beraturan kecepatannya tergantung pada

persamaan kecepatan linier pada gerak melingkar adalah *

apa yang dimaksud dengan gerak parabola

percepatan sudut

rumus kecepatan linear

contoh soal gerak melingkar beraturan beserta jawabannya

contoh soal gerak melingkar beserta jawabannya

soal pilihan ganda gerak melingkar berubah beraturan

soal gerak melingkar kelas 10

soal dan pembahasan gerak melingkar pdf

contoh gerak melingkar beraturan

soal essay dan pembahasan gerak melingkar

pertanyaan tentang gerak melingkar

Pelajari

Pelajaran Matematika Fungsi Komposisi Dan Fungsi Invers

Fungsi Invers 

Dalam matematika suatu fungsi, a, dikatakan invers dari fungsi lainnya, b, jika diberikan keluaran dari b a mengembalikan nilai masukan yang diberikan kepada b. Selain itu, ini harus berlaku untuk setiap elemen dalam domain bersama (rentang) dari b. Dengan kata lain, dengan asumsi x dan y adalah konstanta, jika b(x) = y dan a(y) = x maka fungsi a dikatakan invers dari fungsi b.

Apa itu Fungsi Invers?

Fungsi invers adalah fungsi yang dapat dibalik menjadi fungsi lain. Dengan kata lain, jika sembarang fungsi “f” mengambil p ke q maka, invers dari “f” yaitu “f-1” akan membawa q ke p. Sebuah fungsi menerima nilai yang diikuti dengan melakukan operasi tertentu pada nilai-nilai ini untuk menghasilkan output. Jika mempertimbangkan fungsi, f dan g adalah invers, maka f(g(x)) sama dengan g(f(x)) yang sama dengan x.

Contoh Fungsi Invers

Pertimbangkan fungsi a(x) = 5x + 2 dan b(y) = (y-2)/5. Di sini fungsi b adalah fungsi invers dari a. Kita bisa melihat ini dengan memasukkan nilai ke dalam fungsi. Misalnya ketika x adalah 1 output dari a adalah a(1) = 5(1) + 2 = 7. Menggunakan output ini sebagai y dalam fungsi b menghasilkan b(7) = (7-2)/5 = 1 yang nilai masukan untuk fungsi a.

Sifat Fungsi Invers

Dua fungsi f dan g dikatakan saling invers jika dan hanya jika:

f dan g keduanya adalah fungsi satu-satu. Fungsi One to One memetakan setiap nilai dalam domainnya ke tepat satu nilai dalam co-domain(rentang). Contoh fungsi One to One adalah f(x) = x

Kodomain(rentang) dari f adalah domain dari g dan sebaliknya

Catatan: Beberapa fungsi hanya dapat dibalik untuk sekumpulan nilai tertentu dalam domainnya. Dalam hal ini baik range dan domain dari fungsi invers dibatasi hanya pada nilai-nilai tersebut.

Fungsi Gabungan

Fungsi komposit adalah fungsi yang inputnya adalah fungsi lain. Jadi, jika kita memiliki dua fungsi A(x), yang memetakan elemen dari himpunan B ke himpunan C, dan D(x), yang memetakan dari himpunan C ke himpunan E, maka gabungan dari kedua fungsi ini, ditulis sebagai DoA, adalah fungsi yang memetakan elemen dari B ke E yaitu DoA = D(A(x)).

Sebagai contoh perhatikan fungsi A(x) = 5x + 2 dan B(x) = x + 1. Fungsi komposit AoB = A(B(x)) = 5(x+1) + 2.

Sifat Fungsi Komposit

Fungsi komposit memiliki sifat-sifat berikut:

Mengingat fungsi komposit fog = f(g(x)) co-domain dari g harus menjadi subset, yaitu subset tepat atau tidak tepat, dari domain f

Fungsi komposit bersifat asosiatif. Mengingat fungsi komposit a o b o c urutan operasi tidak relevan yaitu (a o b) o c = a o (b o c).

Fungsi komposit tidak komutatif. Jadi AoB tidak sama dengan BoA. Menggunakan contoh A(x) = 5x + 2 dan B(x) = x + 1 AoB = A(B(x)) = 5(x+1) + 2 sedangkan BoA = B(A(x)) = ( 5x + 2) + 1.

Apa itu fungsi komposit? Nah, fungsi komposit biasanya terdiri dari fungsi lain sedemikian rupa sehingga output dari satu fungsi adalah input dari fungsi lainnya. Dengan kata lain, ketika nilai suatu fungsi ditemukan dari dua fungsi lain yang diberikan dengan menerapkan satu fungsi ke variabel independen dan yang lainnya ke hasil fungsi lain yang domainnya terdiri dari nilai-nilai variabel independen yang hasilnya dihasilkan oleh fungsi pertama terletak di domain kedua.

Contoh: Dua fungsi - 3y+5 dan y2 bersama-sama membentuk fungsi komposit yang dapat ditulis sebagai (3y+5)2

Penjelasan Fungsi Komposisi

Untuk membentuk fungsi komposit dengan komposisi dua fungsi lain, kita perlu mengambil dua fungsi, katakanlah g(x) = [Kesalahan Pemrosesan Matematika], dan f(x) = x+5. Sekarang, kita perlu memasukkan satu fungsi ke dalam fungsi lainnya sehingga di sini kita dapat memasukkan f(x) ke dalam g(x) untuk membentuk fungsi baru, yang disebut komposisinya.

Seperti disebutkan di atas, untuk membentuk fungsi komposit kita perlu memasukkan satu fungsi ke fungsi lainnya. Di sini f(x) dapat dihubungkan ke g(x) untuk membentuk fungsi g(f(x)). Kita tahu bahwa f(x) = x + 5, sehingga kita dapat mensubstitusikan fungsi tersebut ke dalam. Oleh karena itu, g(f(x)) = g(x + 5). Mengetahui fakta bahwa g(x) = [Kesalahan Pemrosesan Matematika]

 kita dapat menyisipkan fungsi dan mengevaluasi g(x + 5) = [Kesalahan Pemrosesan Matematika]

Oleh karena itu, g(f(x)) = g(x + 5) = [Kesalahan Pemrosesan Matematika]

Untuk latihan, unduh contoh komposisi fungsi dengan jawaban pdf. Dengan mengunduh contoh komposisi fungsi dengan jawaban pdf, Anda akan memiliki cukup pertanyaan fungsi komposit untuk dipraktikkan.

Properti Fungsi Komposit

Ada empat sifat utama dari fungsi komposit:

Properti 1: Fungsi komposit tidak komutatif

                                 gof tidak sama dengan fog

Properti 2: Fungsi komposit bersifat asosiatif

                   (fog)oh = fo(goh)

Sifat 3: Sebuah fungsi f: A -B dan g: B-C adalah satu-satu maka gof: A-C juga satu-satu.

Sifat 4: A fungsi f: A-B dan g: B-C on lalu gof: A-C juga on.

Agar lebih terang benderang lagi kita menusu soal dan pembahasan, selengkapnya:

Soal Fungsi Komposisi Dan Fungsi Invers

Tag:

soal dan pembahasan fungsi komposisi dan fungsi invers doc

contoh soal fungsi komposisi dan fungsi invers dalam kehidupan sehari-hari

contoh soal fungsi komposisi dan fungsi invers

contoh soal fungsi komposisi

soal hots fungsi komposisi dan invers

soal cerita fungsi komposisi

komposisi fungsi dan fungsi invers kelas 11

penjumlahan fungsi komposisi

Pelajari

Pelajaran Matematika Pertidaksamaan Irasional

Pertidaksamaan Irasional adalah bentuk pertidaksamaan, yang memiliki fungsi dalam tanda akar baik fungsi di ruas kiri, fungsi di ruas kanan atau di kedua ruasnya. Pertidaksamaan irasional terdefinisi jika syarat-syaratnya terpenuhi yaitu jika fungsi dalam akar besarnya lebih besar atau sama dengan nol

Apa Definisi singkat Pertidaksamaan Irasional: 

• Pertidaksamaan irasional adalah pertidaksamaan yang memuat variabel di bawah tanda akar-derajat.

Apa Definisi Pertidaksamaan?

• Pertidaksamaan adalah hubungan yang membuat perbandingan tidak sama antara dua angka atau ekspresi matematika lainnya. 

Apa aturan ketidaksetaraan?

Aturan untuk Memecahkan Pertidaksamaan

• Tambahkan nomor yang sama di kedua sisi.
• Dari kedua sisi, kurangi angka yang sama.
• Dengan bilangan positif yang sama, kalikan kedua ruas.
• Dengan bilangan positif yang sama, bagi kedua ruas.
• Kalikan angka negatif yang sama di kedua sisi dan balikkan tandanya.

Apa definisi Irasional?

• Irasional adalah semua bilangan real yang bukan bilangan rasional. Artinya, bilangan irasional tidak dapat dinyatakan sebagai rasio dua bilangan bulat.
• 
  

Untuk lebih jelasnya silahkan pelajari Soal dan Pembahasan

Soal Pertidaksamaan Irasional

Tag:

mengapa pertidaksamaan irasional menggunakan tanda akar

pertidaksamaan rasional dan irasional

carilah contoh soal dan penyelesaiannya mengenai pertidaksamaan irasional

irasional adalah

soal pertidaksamaan irasional beserta jawabannya

soal pertidaksamaan irasional pdf

soal pertidaksamaan irasional kelas 10

contoh soal irasional

10 contoh soal pertidaksamaan irasional

contoh soal pertidaksamaan irasional

contoh soal pertidaksamaan irasional pecahan

pertidaksamaan irasional bentuk akar

Pelajari